这篇文章刚出来那几天,正好比较忙。这两天,抽空把这篇文章读了一下。以下是简要的读书笔记。这篇文章包含附录长达97页。其中正文40多页。
这篇文章在非正式场合宣传中(如微博微信或公众号),经常被称为”从第一性原则出发的深度网络“。但是,也受到一些批评。第一性原则是一个foundermental的原则,例如物理中的对称原则(能量守恒定律、宇称守恒定律),用这个词来刻画本文,可能有点浮夸。
ReduNet: A White-box Deep Network from the Principle of Maximizing Rate Reduction
从最大下降率原则出发的一种白盒深度神经网络。
maximizes the coding rate difference between the whole dataset and the average of all the subsets
最大化“整体数据集” "所有子集的平均"之间的编码率差异
constructed layer-by-layer via forward propagation, instead of learned via back propagation
逐层搭建,只前向,不后向
What exactly do we try to learn from and about the data?
我们究竟想从数据中学习什么
我们想从数据中学习什么样的表示?我们需要构建什么样的网络来实现这个目标
learn a low-dimensional linear discriminative representation of the data:
目标是学习低维线性判别性特征
rate reduction
运价减成理论可以解决这个问题。
where within-class variability and structural information are completely suppressed and ignored
cross entropy loss有各种问题。其中一个问题是,类内的差异性和结构信息会被抑制和忽略。
neural collapsing phenomenon. That is, features of each class are mapped to a one-dimensional vector whereas all other information of the class is suppressed.
分类最终用一维来表达会出现上述的神经崩溃问题。
The precise geometric and statistical properties of the learned features are also often obscured,
所学习到的特征会缺乏几何特性和统计特性
Formally, it seeks to maximize the mutual information I(z, y) (Cover and Thomas, 2006) between z and y while minimizing I(x, z) between x and z:
x -> z > y
最大化 z和y之间的互信息
最小化x和z之间的互信息?
和vae那么像?
our framework uses the label y as only side information to assist learning distcriminative yet diverse (not minimal) representations; these representations optimize a different intrinsic objective based on the principle of rate reduction
所以这篇文章只是用标签来做一个辅助信息来学习特征。
Typically, such representations are learned in an end-to-end fashion by imposing certain heuristics on geometric or statistical “compactness” of z
autoencoder也有类似的功能
fail to capture all internal subclass structures or to explicitly discriminate among them for classification or clustering purposes.
但是自编码可能会对类问题的区分没学习好。
model collapsing in learning generative models for data that have mixed multi-modal structures
所以自编码可能带来模型崩溃的问题(交叉熵会带来神经崩溃的问题)。
If the above contractive learning seeks to reduce the dimension of the learned representation, contrastive learning (Hadsell et al., 2006; Oord et al., 2018; He et al., 2019) seems to do just the opposite
然后这里又讨论了对比学习(这篇文章好像把各种工作的拉进来讨论,想做一个通用性的东西)。
contractive learning and contrastive learning,
这篇文章把自编码相关工作称为收缩学习,自监督学习称为对比学习(可能是为了单词的对称之美)。
As we may see from the practice of both contractive learning and contrastive learning, for a good representation of the given data, people have striven to achieve certain tradeoff between the compactness and discriminativeness of the representation. Contractive learning aims to compress the features of the entire ensemble, whereas contractive learning expands features of any pair of samples. Hence it is not entirely clear why either of these two seemingly opposite heuristics seems to help learn good features. Could it be the case that both mechanisms are needed but each acts on different part of the data? As we will see, the rate reduction principle precisely reconciles the tension between these two seemingly contradictory objectives by explicitly specify to compress (or contract) similar features in each class whereas to expand (or contrast) the set of all features in multiple classes。其中:
Contractive learning aims to compress the features of the entire ensemble,
自编码收缩特征,而
, whereas contractive learning expands features of any pair of samples.
对比学习扩张特征。
As we will see, the rate reduction principle precisely reconciles the tension between these two seemingly contradictory objectives by explicitly specify to compress (or contract) similar features in each class whereas to expand (or contrast) the set of all features in multiple classes
本文提出的方法可以综合这两方面的优劣。可以收缩同类的特征(那岂不是又落入cross entropy的缺点里面?),而扩张不同类的特征。
So, how do we design a neural networks?
那么,我们要怎么设计神经网络呢?
Design a network
设计一个网络
or search for a neural networks
网络结构搜索
there has been apparent lack of direct justification of the resulting network architectures from the desired learning objectives, e.g. cross entropy or contrastive learning.
问题在于,利用cross entropy和对比学习做目标来设计神经网络结构是未必准确的。作者认为,自己提出的方法相对这些目标,可行一些。
To a large extent, this work will resolve this issue and reveal some fundamental relationships between sparse coding and deep representation learning.
这篇文章从一个很高的程序,解释了sparse coding与深度表达学习之间的关系 。
However, in both cases the forward-constructed networks seek a representation of the data that is not directly related to a specific (classification) task. To resolves limitations of both the ScatteringNet and the PCANet, this work shows how to construct a data-dependent deep convolution network in a forward fashion that leads to a discriminative representation directly beneficial to the classification task.
这篇文章认为,用到标签信息是坏事。所以这篇文章的思想自监督学习有莫大的关联。
To do so, we require our learned representation to have the following properties, called a linear discriminative representation (LDR):
压缩编码想要线性可分。类内压缩/类内可分/还要deverse
Here, however, although the intrinsic structures of each class/cluster may be low-dimensional, they are by no means simply linear (or Gaussian) in their original representation x and they need be to made linear through a nonlinear transform z = f(x).
Unlike LDA (or similarly SVM), here we do not directly seek a discriminant (linear) classifier. Instead, we use the nonlinear transform to seek a linear discriminative representation7 (LDR) for the data such that the subspaces that represent all the classes are maximally incoherent.
那么,它和LDA/SVM就很像了。不过还是有区别的:LDA是用线性提一个特征,然后加一个非线性核,最后线性可分。而这篇文章,并不是用一个线性来提特征。这篇文章直接用一个非线性映射(如神经网络)来提一个特征,然后线性分类。(注:这个区别好像不明显。对LDA而言,我们可以认为加了非线性核之后才是相想的特征,这样来看,这篇文章的方法就和它们没有区别了)
In this paper, we attempt to provide some answers to the above questions and offer a plausible interpretation of deep neural networks by deriving a class of deep (convolution) networks from first principles. We contend that all key features and structures of modern deep (convolution) neural networks can be naturally derived from optimizing the rate reduction objective, which seeks an optimal (invariant) linear discriminative representation of the data. More specifically, the basic iterative projected gradient ascent scheme for optimizing this objective naturally takes the form of a deep neural network, one layer per iteration.
这篇文章称,它从第一性原理的角度,解释了神经网络。
is there a simple but principled objective that can measure the goodness of the resulting representations in terms of all these properties? The key to these questions is to find a principled “measure of compactness” for the distribution of a random variable z or from its finite samples Z
如何衡量紧凑性
To alleviate this difficulty, another related concept in information theory, more specifically in lossy data compression, that measures the “compactness” of a random distribution is the so-called rate distortion (Cover and Thomas, 2006):
比率失真可以衡量紧凑性
Given a random variable z and a prescribed precision eps > 0, the rate distortion R(z, eps) is the minimal number of binary bits needed to encode z such that the expected decoding error is less than , i.e., the decoded zb satisfies E[kz − zbk2] ≤ eps
比率失真:给定一个eps,最小需要多少比特的编码
Therefore, the compactness of learned features as a whole can be measured in terms of the average coding length per sample (as the sample size m is large), a.k.a. the coding rate subject to the distortion:
综上,紧凑性可以所有样本的平均编码长度来衡量。
In general, the features Z of multi-class data may belong to multiple low-dimensional subspaces. To evaluate the rate distortion of such mixed data more accurately, we may partition the data Z into multiple subsets:
如果含有多个类别的话,则每一类都分开搞,然后求平均。
Shortly put, learned features should follow the basic rule that similarity contracts and dissimilarity contrasts.
学习的过程和一般的metric learning基本一样。
To be more precise, a good (linear) discriminative representation Z of X is one such that, given a partition Π of Z, achieves a large difference between the coding rate for the whole and that for all the subsets:
很棒,这个公式和我们当年的triplet loss有异曲同工之秒。它最大化整体的code rate(diverse),最小化类内的code rate。(但问题也来了,这使得类内的差异性变小,出现了作者claim的cross entropy的问题:类内的差异性和结构信息会被抑制和忽略。前后文矛盾了)
In this work, to simplify the analysis and derivation, we adopt the simplest possible normalization schemes, by simply enforcing each sample on a sphere or the Frobenius norm of each subset being a constant
在这一段里面,作者和bn拉了一下关系。最终作者采用的是l2 norm,这些规范化技术在triplet loss和contrastive learning中是很常用的。
We refer to this as the principle of maximal coding rate reduction (MCR2 ), an embodiment of Aristotle’s famous quote: “the whole is greater than the sum of the parts.”
虽然作者用了the whole is greater than the sum of the parts来解释,但我更偏向用”最大化整体的code rate(diverse),最小化类内的code rate“来解释。
另外一个问题来了:用mcr2类似于triplet loss,这就是文章前文所称的"所以这篇文章只是用标签来做一个辅助信息来学习特征"吗?这个似乎不太严谨。
MCR2 focuses on learning representations z(θ) rather than fitting labels.
所以,这个Claim也有一定的争议。
The maximal coding rate reduction can be viewed as a generalization to information gain (IG), which aims to maximize the reduction of entropy of a random variable, say z, with respect to an observed attribute, say π: maxπ IG(z,π) .= H(z) − H(z | π), i.e., the mutual information between z and π (Cover and Thomas, 2006). Maximal information gain has been widely used in areas such as decision trees (Quinlan, 1986).
确实看形式来说,MCR2和互信息有一定的联系。全体与局部的互信息。
We here reveal nice properties of the optimal representation with the special case of linear subspaces, which have many important use cases in machine learning
我们将介绍MCR的美丽性质。
Between-class Discriminative:
As long as the ambient space is adequately large (n ≥ k j=1 dj ), the subspaces are all orthogonal to each other
类间两两正交
Maximally Diverse Representation:
差异性最大化
In other words, the MCR2 principle promotes embedding of data into multiple independent subspaces,14 with features distributed isotropically in each subspace (except for possibly one dimension). In addition, among all such discriminative representations, it prefers the one with the highest dimensions in the ambient space
本文的方法可以更好的保证每一类的空间比较正交,且偏好维度更高。传统的cross entropy无法做到这样。
Orthogonal low-rank embedding (OLE) loss。∆R, OLE is always negative and achieves the maximal value 0 when the subspaces are orthogonal, regardless of their dimensions. So in contrast to ∆R, this loss serves as a geometric heuristic and does not promote diverse representations. In fact, OLE typically promotes learning one-dim representations per class, whereas MCR2 encourages learning subspaces with maximal dimensions (Figure 7 of Lezama et al. (2018) versus our Figure 17).
和OLE的区别是:OLE和cross entropy一样,偏向把维度弄成1,也就是前面所说的作者claim的cross
entropy的问题:类内的差异性和结构信息会被抑制和忽略。(我不太赞同这个观点。就算是cross
entropy,我们所说的特征是指分类前一层。真的前一层会偏向把维度变成1吗?有实验经验的朋友会马上回答”No“。总之,作者cross-entropy的缺点时,前后文时常相互矛盾,有时指分类的前一层特征,有时有想用分类层来解释。)
Relation to contractive or contrastive learning.
本文的方法和对比学习(以及作者用的收缩学习这个词)和很大的相关性。尤其是与逐层对比学习相关性极大。我认为,对比学习可能优于本文的方法。本文认为,所提的方法可以与对比学习相结合。
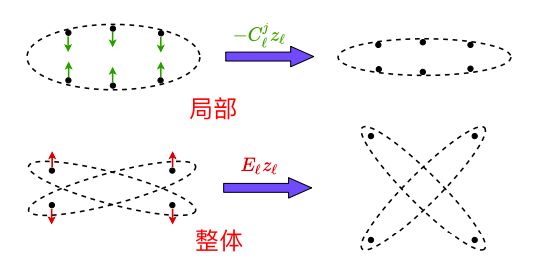
That is, we need to approximate the gradient flow ∂∆R ∂Z that locally deforms all (training) features {z i ` } m i=1 with a continuous mapping g(z) defined on the entire feature space z` ∈ R n
梯度只局限于各个类内不好(说得不是很清楚为什么局限于类内),需要要加一项
Remark 3 (Approximate Membership with a ReLU Network) The choice of the softmax is mostly for its simplicity as it is widely used in other (forward components of ) deep networks for purposes such as clustering, gating (Shazeer et al., 2017) and routing (Sabour et al., 2017). In practice, there are many other simpler nonlinear activation functions that one can use to approximate the membership πb(·) and subsequently the nonlinear operation σ in (24). Notice that the geometric meaning of σ in (24) is to compute the “residual” of each feature against the subspace to which it belongs. There are many different ways one may approximate this quantity. For example, when we restrict all our features to be in the first (positive) quadrant of the feature space,18 one may approximate this residual using the rectified linear units operation, ReLUs, on pj = C j ` z` or its orthogonal complement:
这篇文章实际用了神经网络来实现它。
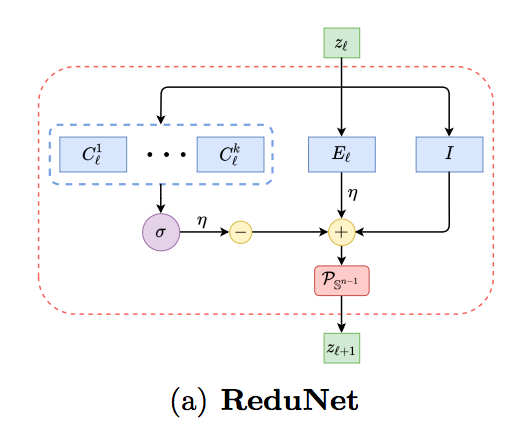
网络结构如上图所示。其实简单来说,就是k个非线性换(可认为是conv或fc+relu,其参数是C1到Ck),一个线性变换(可视为conv或fc,无激活函数,其参数为E),和一个identity(shortcut)。其中P代表着,l2规范化。

训练算法如上图所示。其中,第5行代表着,每一次迭代后,网络参数C和E可以直接计算得到。测试和训练基本一致。只不过测试的时候,不需要更新参数。所以测试时,第5行是没有的。
In our experiments (see Section 5), we have observed that the basic gradient scheme sometimes converges slowly, resulting in deep networks with hundreds of layers (iterations)! To improve the efficiency of the basic ReduNet, one may consider in the future accelerated gradient methods such as the Nesterov acceleration (Nesterov, 1983) or perturbed accelerated gradient descent (Jin et al., 2018). Say to minimize or maximize a function h(z), such accelerated methods usually take the form。
大家可以看到,前面的训练算法框架中,并没有BP。也就是网络是逐层前向传播,不需要反向的,因为每一次迭代后,网络参数C和E可以直接计算得到。不过,这里,作者指出,这样收敛很慢。所以,可以采样每一层先前向,后反向,再更新参数。这样,就与文章所claim的本文方法透明可解释,只前向不反向有点混淆。不过,在我看来,就算是每层BP进行梯度下降,也不影响本文所claim的内容。因为一层的BP,不应该看作是BP算法。这就是正常的梯度下降。
Of course, like any other deep networks, the so-constructed ReduNet is amenable to fine-tuning via back-propagation if needed. A recent study from Giryes et al. (2018) has shown that such fine-tuning may achieve a better trade off between accuracy and efficiency of the unrolled network (say when only a limited number of layers, or iterations are allowed in practice). Nevertheless, for the ReduNet, one can start with the nominal values obtained from the forward construction, instead of random initialization. Benefits of fine-tuning and initialization will be verified in the experimental section (see Table 2).
大家会问一个问题,为什么要这么费劲?如果直接end-to-end 将所有层合在一块进行BP求解,会变好吗?作者指出,先用本文的方法进行逐层训练,然后再合在一块BP,也是可以的。效果确实会提升。
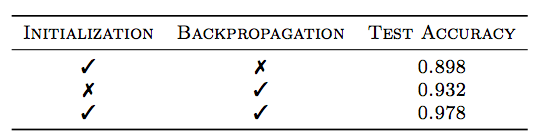
这篇文章实验相对比较弱。只是在CIFAR-10做了一些小分析。公布有效结果的只有这个MNIST的表格。第一行代表本文方法的效果。第二行代表BP方法的效果。第三行代表先用本文方法训练,作为初始化,再用BP进行finetune的效果。虽然第三行确实比第二行高了不少。但是,可能比较不太合理。比较公平的方案是,第二行应该拉长训练时间,使得BP的时间(epoch) = 用本文方法初始化的epoch + BP finetune的epoch。也许公平来比较,本文的方法是比不过BP的。
-----------------------------------
大家好,我来自fast lab。我开始不定时公开写作。这些写作主要通过两个渠道公布:一是FAST LAB官方网站;一是印象识堂(微信可访问)。欢迎大家订阅。谢谢!
FAST Lab的官方网址为:https://wanggrun.github.io/projects/fast
除此外,还可以关注我的小伙伴王广润:https://wanggrun.github.io/
王广聪: https://wanggcong.github.io/
石阳:https://www.linkedin.com/in/%E9%98%B3-%E7%9F%B3-381b521a4/
有时候这些网站打不开,请耐心多点几次。
多谢大家关注。